Kattis – fenwick

Today’s problem is quite exciting because I get to learn a new, cool data structure: the Fenwick (BIT) tree. Since its a new data structure, I have only done the Entry Level problem from halim.

Fenwick Tree

This structure is used for fast $O(m\log m)$ dynamic prefix sum queries, where $m$ is the length of the underlying array. In problem solving, the underlying array is frequently a frequency array.

It makes frequent use of the LSOne operation (see coding-11).

structure

The Fenwick tree is essentially a tree whose parents and children are linked together by the LSOne(S) operation. This relationship is special because each branch of the Fenwick tree will cover the full range from [1...i] where i is the index of the last node. With each node in the Fenwick Tree being itself the cumulative frequency of the underlying array f till the index of its parent.

Here the last node is the index with only one 1 in its binary representation. To borrow a diagram from halim, the structure of the Fenwick tree is as such:

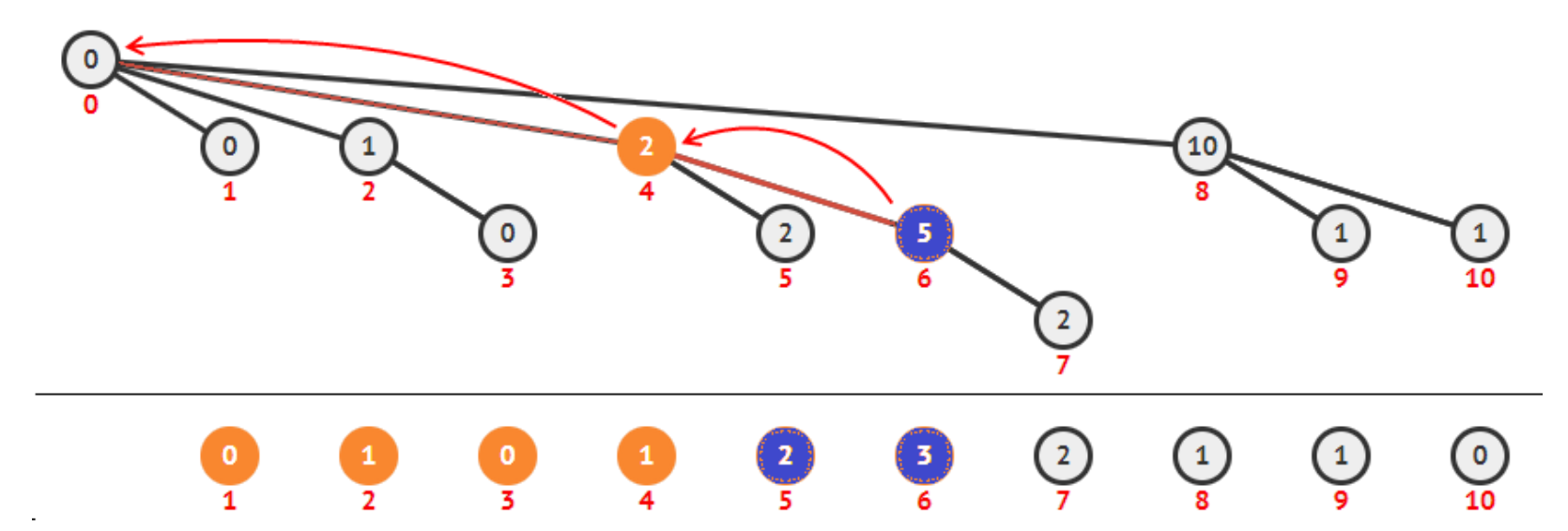
basic operations

The Fenwick Tree supports 2 basic operations:

• update(i, v): update element i in underlying array with v (i.e. a[i] += v)
• rsq(j): find the prefix sum in range [1...j]
  • this operation gives the range [i...j] trivially, i.e. rsq(i,j) = rsq(j) - rsq(i-1)

implementation

The bare-bones implementation of the Fenwick Tree is quite simple and easy to remember:

#define LSOne(S) ((S) & -(S))

#typedef vector<int> vi;

class fenwick_tree {
	private:
		vi ft;
	public:
		fenwick_tree(int m) { ft.assign(m + 1, 0); }
		void update(int i, int v) {
			for (; i < (int) ft.size(); i += LSOne(i))
				ft[i] += v;
		}
		int rsq(int j) {
			int acc = 0;
			for (; j > 0; j -= LSOne(S)) {
				acc += ft[j];
			}
			return acc;
		}
		int rsq(int i, int j) { return rsq(j) - rsq(i - 1); }
}

expansions

There are many expansions to the Fenwick Tree to optimize other common operations. I plan to explore those in the next few daily-codings.

my solution (to Kattis – fenwick)

#include <bits/stdc++.h>

using namespace std;

#define LSOne(S) ((S) & -(S))

typedef vector<long long> vi;

class FenwickTree {
    private:
        vi ft;

    public:
        FenwickTree(int m) { ft.assign(m + 1, 0); }

        void update(int i, int v) {
            for (; i < (int) ft.size(); i += LSOne(i))
                ft[i] += v;
        }
        
        long long rsq(int i) {
            long long acc = 0;
            for(; i > 0; i -= LSOne(i))
                acc += ft[i];
            return acc;
        }
};

int main() {
    ios::sync_with_stdio(0);
    cin.tie(0); cout.tie(0);

    int N, Q, i, e;
    char op;
    
    cin >> N >> Q;

    FenwickTree ft(N);

    while (Q--) {
        cin >> op;
        switch(op) {
            case '+':
                cin >> i >> e;
                ft.update(i + 1, e);
                break;
            case '?':
                cin >> i;
                cout << ft.rsq(i) << "\n";
                break;
        }
    }

    return 0;
}